PCA(주성분 분석)

PCA는 내가 가진 데이터에서 가장 중요한 성분을 순서대로 추출하는 기법이다.

• 내 데이터의 분산을 가장 잘 설명해주는 축이 주성분1(PC1)
• PC1에 직교하는 축이 주성분2(PC2)

이미지 데이터에서 사용하는 PCA

공분산 행렬은 데이터 간 퍼져있는 정도를 나타내는 행렬

 

PCA는 분산을 최대화 하는축(주성분)을 찾는 작업이다

 

공분산행렬

Eigenvalue(고유값) & Eigenvector(고유벡터)

 

공분산 행렬에서 나타나는 고유한 벡터와 벡터의 고유값을 의미한다.

 

고유한 벡터: 분산의 방향, 주성분

 

벡터의 고유값: 분산의 크기, 주성분의 연산

 

v는 0이 아니어야한다. I는 단위행열이다. 역행렬이 존재하면 안되는 걸 찾는것. 

 

Eigenvalue의  크기 순서대로 eigenvector을 나열한다.

정렬된 eigenvector 중 필요한 만큼 일부 선택하여 차원축소를 한다.

 

필요한 만큼이 얼마일까?

 

주성분의 개수설정하는것을 알아보자 3가지 방법이있다.

 

1. 시각화를 위해 2 or 3 개로 주성분 개수를 설정한다.(2차원 or 3차원) = 3차원 이상이면 시각화할수가 없다.
2. Eigenvalue>1을 기준으로 주성분 개수를 설정한다.
3. 주성분 개수가 늘어나도 분산이 더이상 추가되지 않는 지점에서 주성분 개수를 설정한다.

이제 실습을 해보자

 

오늘 사용할 데이터는 머신러닝에서 예제로 자주 사용되는 iris 꽃 데이터이다.

 

데이터를 살펴보자

head(iris)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

 

colSums(is.na(iris))

colSums 함수 = 각 변수별로 

is.na함수 = 결측치가 있는지

 

summary(iris)

  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  

species는 범주형 변수라서 카운트 된 값이 나온다.

보통 데이터를 볼때 Median과 Mean를 주로 보는데 둘의 차이가 많으면 outlier 값이 많은것이기 때문!

 

boxplot(iris[,1:4])

데이터의 형태를 알아보기 위해 boxplot을 이용해서 나타낸다.

species는 범주형이기 때문에 제외하고 나타냈다.

 

iris.pca <- prcomp(iris[1:4],center = T, scale. = T) #PCA 함수

 pca 함수는 한줄이면 된다.

iris데이터의 1열부터 4열 까지, center = T, scale = T 은 평균은 0 분산은 1로 표준화를 해줘라 라는뜻이다.

 

 

summary(iris.pca)

Importance of components:
                          PC1    PC2     PC3     PC4
Standard deviation     1.7084 0.9560 0.38309 0.14393 #표준편차 표준편차를 제곱하면 분산 = eigenvalue
Proportion of Variance 0.7296 0.2285 0.03669 0.00518 #분산이 전체분산에서 차지하는 비율
Cumulative Proportion  0.7296 0.9581 0.99482 1.00000 #누적분산의 비율

 

iris.pca$rotation #각 주성분의 eigenvector

                    PC1         PC2        PC3        PC4
Sepal.Length  0.5210659 -0.37741762  0.7195664  0.2612863
Sepal.Width  -0.2693474 -0.92329566 -0.2443818 -0.1235096
Petal.Length  0.5804131 -0.02449161 -0.1421264 -0.8014492
Petal.Width   0.5648565 -0.06694199 -0.6342727  0.5235971

 

eigenvector = 각 변수들의 가중치

 

head(iris.pca$x,10) #각 주성분의 값

            PC1         PC2         PC3          PC4
 [1,] -2.257141 -0.47842383  0.12727962  0.024087508
 [2,] -2.074013  0.67188269  0.23382552  0.102662845
 [3,] -2.356335  0.34076642 -0.04405390  0.028282305
 [4,] -2.291707  0.59539986 -0.09098530 -0.065735340
 [5,] -2.381863 -0.64467566 -0.01568565 -0.035802870
 [6,] -2.068701 -1.48420530 -0.02687825  0.006586116
 [7,] -2.435868 -0.04748512 -0.33435030 -0.036652767
 [8,] -2.225392 -0.22240300  0.08839935 -0.024529919
 [9,] -2.326845  1.11160370 -0.14459247 -0.026769540
[10,] -2.177035  0.46744757  0.25291827 -0.039766068

plot(iris.pca, type = 'l', main = 'Scree Plot') #PC의 분산을 y축으로 scree plot 생성

주성분의 개수를 선택하기 위해 Scree Plot을 그려본다.

옵션중에 type = 'l' 은 line을 의미한다.

 

 

여기서 elbow point는 3이다.

하지만 variances = eigenvalue 가 1보다 커야하므로  2일때가 적당하다.

 

head(iris.pca$x[,1:2], 10) #2열까지 가져오며 2차원으로 축소

 시각화를 해보자

library(ggfortify)

autoplot(iris.pca,data = iris, colour = 'Species') 

autoplot에 data = iris, colour 을 넣은건 레이블을 같이 시각화 해줘서 확인하기 위함이다.

 

빨간색 종은 다른 종들과 뚜렷하게 구분이되는 종이다.

 

이번엔 사진 분석을 PCA를 통해 실습해보자

 

오늘 사용할 사진은 귀여운 고양이 사진이다.

 

library(jpeg)

cat <- readJPEG('cat.jpg')
class(cat)

class를 확인해보면 array라고 나온다.

 

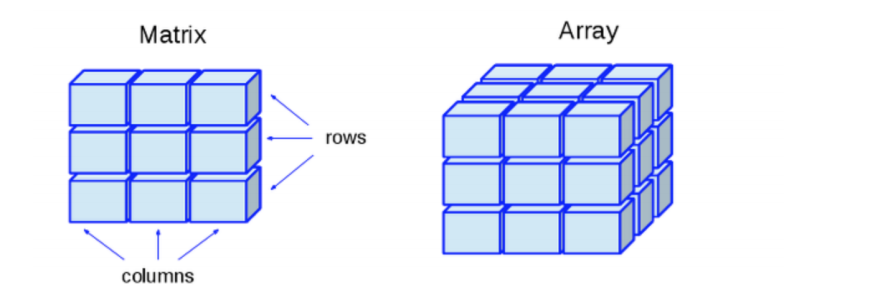
array는 matrix를 몇겹 겹쳐놓은 3차원 데이터이다.

R/G/B가 들어있으므로 3차원이다.

dim(cat)

[1] 360 480   3 # R G B

R G B 를 각자 하나씩 빼면 2차원으로 된다.

r <- cat[,,1] #R에 해당하는데이터
g <- cat[,,2] #G에 해당하는데이터
b <- cat[,,3] #B에 해당하는데이터

cat.r.pca <- prcomp(r,center = F) #r 데이터 주성성분 분석
cat.g.pca <- prcomp(g,center = F) #g 데이터 주성성분 분석
cat.b.pca <- prcomp(b,center = F) #b 데이터 주성성분 분석

rgb.pca <- list(cat.r.pca,cat.g.pca,cat.b.pca) #분석결과 rgb로 합침

pc <- c(2,10,50,100,300) #축소할 차원수

for (i in pc) { 
  pca.img <- sapply(rgb.pca, function(j){  #sapply는 리스트의 각각데이터에 함수를 적용해줌, funtion(j)에서 j = rgb.pca가된다.
    compresssed.img <- j$x[,1:i] %*% t(j$rotation[,1:i]) #주성분의 값 x , rotation = eigenvector 이고 %*%은 행렬곱이다.
  },simplify = 'array'  #array로 만들어줘라
    
    ) 
  writeJPEG(pca.img,paste('cat_pca_',i,'.jpeg',sep = ' ')) #jpeg 파일로 저장한다.
  
  
}

2차원

10차원

50차원

100차원

300차원

300차원이 되고나서야 우리가 처음넣은 사진이랑 비슷하게 나온다.